C++ CS

[Algorithm] 기본 정렬 알고리즘 Sorting

Posted by DHniyeo Blog on April 26, 2024

개요

코딩 테스트에도 간혹 등장하고 정렬하는 모든 방법을 정리해보고자 한다.

알긴 알았어도 사실상 algorithm 라이브러리의 sort를 사용하다 보니 까먹어서 정리하게 되었다.

참고로 algorithm 라이브러리의 sort는 개선된 quick sort와 Tim sort 알고리즘을 선택적으로 사용하는 최적화된 알고리즘이다.

따라서 O(n*logn)의 시간 복잡도를 항상 만족한다.

1. 삽입 정렬 (Insertion sort)

0

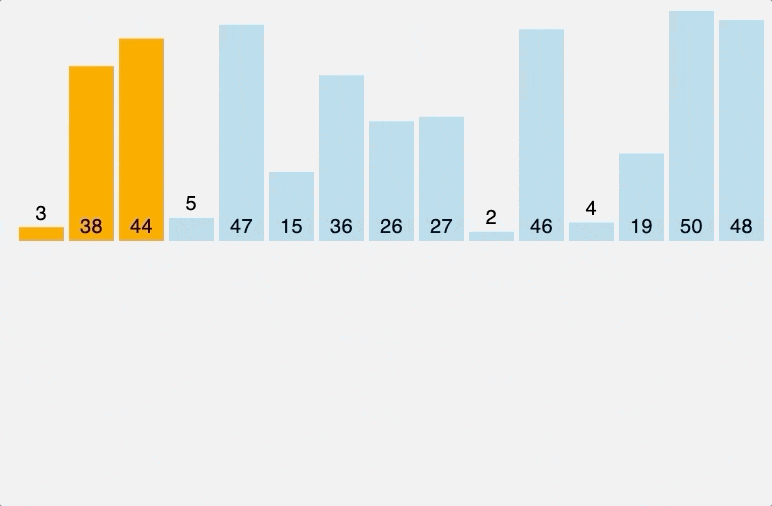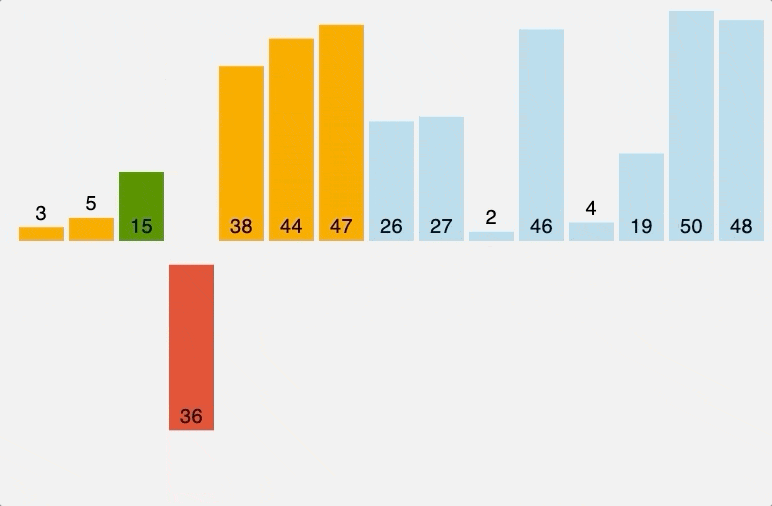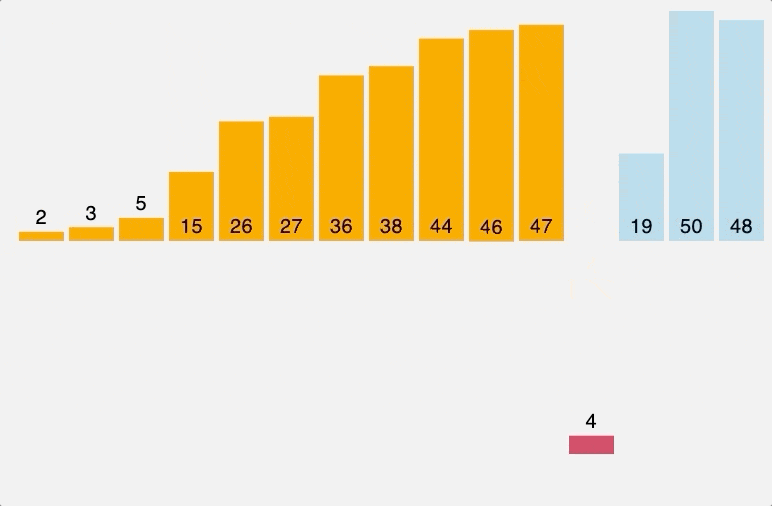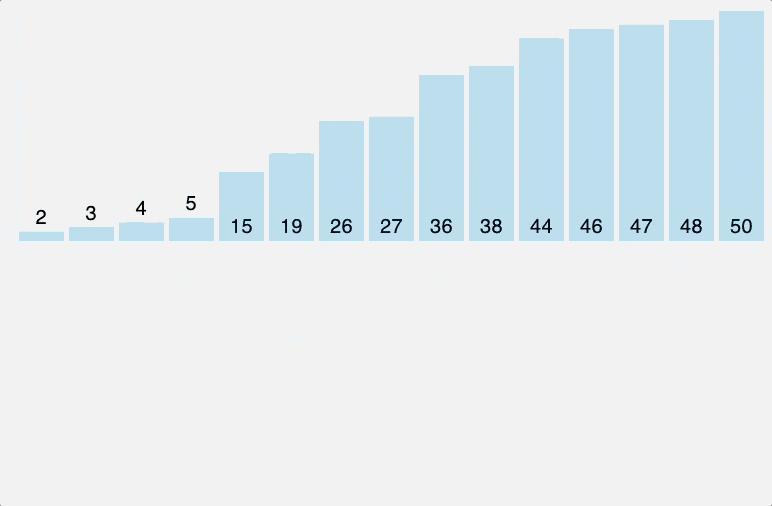
삽입 정렬은 마치 카드 게임에서 카드를 정렬하는 것과 비슷합니다. 이미 정렬된 부분과 비교하여 하나씩 삽입하면서 정렬하는 방식입니다.

1
2
3
4
5
6
7
8
9
10
11
12

  """ Best: O(n) Average: O(n^2) Worst: O(n^2) | O(n) """
void insertionSort(int arr[], int n) {
  for (int i = 1; i < n; i++) {
    int key = arr[i];
    int j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j]; // 뒤로 한칸 뺌
      j--;
    }
    arr[j + 1] = key; // 더 작은값 뒤에 넣어줌
  }
}

장점:

  • 작은 데이터 세트에 효율적입니다.
  • 이미 부분적으로 정렬된 데이터에 효율적입니다.
  • 추가 공간이 필요하지 않습니다.

단점:

  • 다른 정렬 알고리즘들보다 느린 속도입니다.
  • O(n^2)의 시간 복잡도를 가지고 있습니다.

2. 선택 정렬 (Selection sort)

1

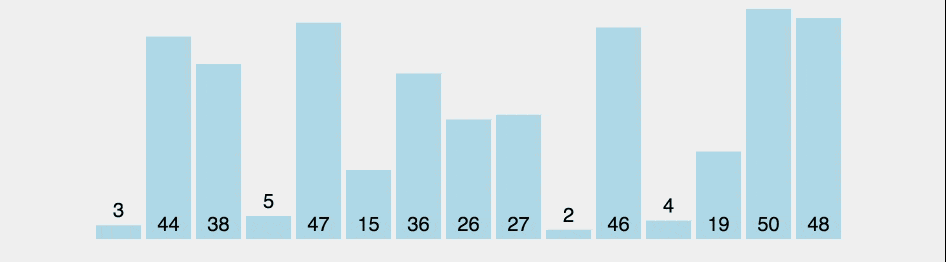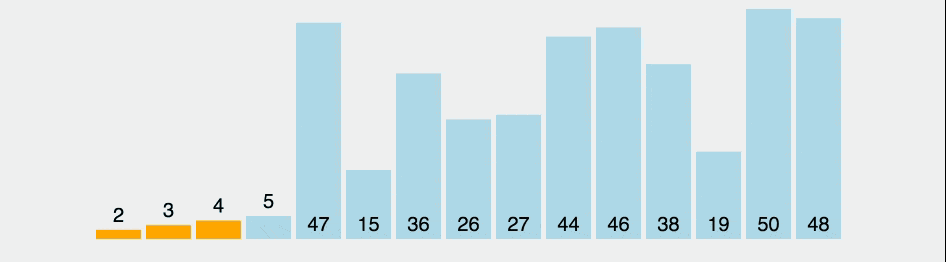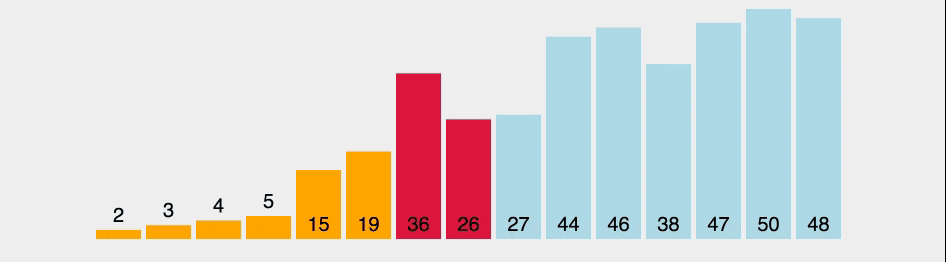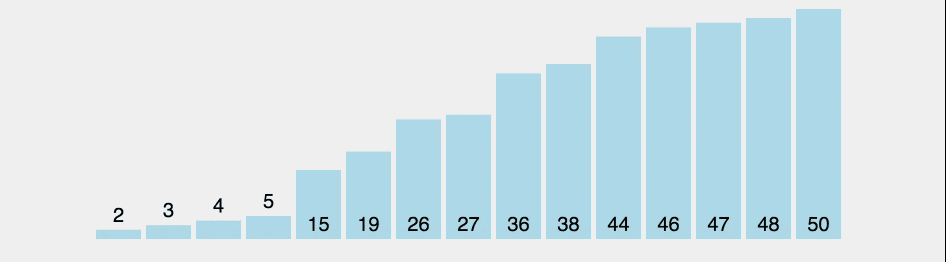
선택 정렬은 가장 작은 요소를 반복적으로 찾아 정렬된 위치에 삽입하는 방식입니다.

1
2
3
4
5
6
7
8
9
10
11

""" Best: O(n^2) Average: O(n^2) Worst: O(n^2) | O(N^2) """
void selectionSort(int arr[], int n) {
  for (int i = 0; i < n - 1; i++) {
    int minIndex = i;
    for (int j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIndex])
        minIndex = j;
    }
    swap(arr[i], arr[minIndex]);
  }
}

장점:

  • 간단한 구현
  • 추가 공간이 필요하지 않습니다.

단점:

  • 다른 정렬 알고리즘들보다 느린 속도입니다.
  • O(n^2)의 시간 복잡도를 가지고 있습니다.

3. 버블 정렬 (Bubble sort)

2

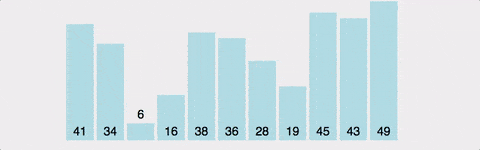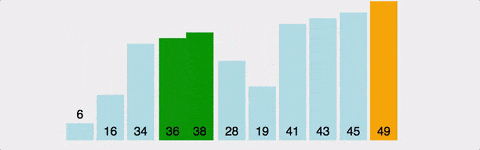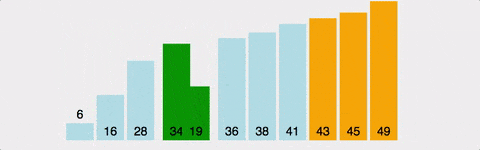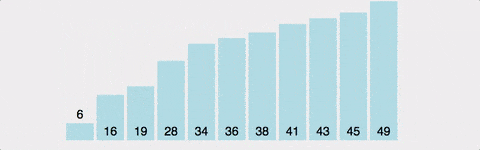
버블 정렬은 인접한 두 요소를 비교하여 큰 값이 뒤쪽으로 이동하도록 반복적으로 교환하는 방식입니다. 마치 물속의 거품이 위로 올라가는 것처럼 큰 값이 점차적으로 올라가는 모습을 띕니다.

1
2
3
4
5
6
7
8
9
10

""" Best: O(n^2) Average: O(n^2) Worst: O(n^2) | O(n) """
void bubbleSort(int arr[], int n) {
  for (int i = 0; i < n - 1; i++) {
    for (int j = 0; j < n - i - 1; j++) { // 뒤쪽에는 정렬이 되있으므로 비교 인덱스가 줄어듦
      if (arr[j] > arr[j + 1]) {
        swap(arr[j], arr[j + 1]);
      }
    }
  }
}

장점:

  • 간단한 구현
  • 추가 공간이 필요하지 않습니다.

단점:

  • 다른 정렬 알고리즘들보다 느린 속도입니다.
  • O(n^2)의 시간 복잡도를 가지고 있습니다.

4. 퀵 정렬 (Quick sort)

3

퀵 정렬은 분할 정복(Divide and Conquer) 알고리즘으로, 다음과 같은 방식으로 작동합니다.

  1. 피벗 요소 선택: 배열에서 임의의 요소를 피벗 요소로 선택합니다.
  2. 분할: 피벗 요소보다 작은 요소들은 피벗 요소 왼쪽, 피벗 요소보다 큰 요소들은 오른쪽으로 분할합니다.
  3. 재귀적 호출: 왼쪽과 오른쪽 부분 배열을 다시 퀵 정렬 알고리즘을 사용하여 재귀적으로 정렬합니다.
  4. 합병: 정렬된 왼쪽, 오른쪽 부분 배열을 합쳐 하나의 정렬된 배열을 만듭니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

""" Best: O(nlogn) Average: O(nlogn) Worst: O(n^2) | O(nlogn) """
void quickSort(int arr[], int low, int high) {
  if (low < high) {
    int pi = partition(arr, low, high);
    quickSort(arr, low, pi - 1);
    quickSort(arr, pi + 1, high);
  }
}

int partition(int arr[], int low, int high) {
  int pivot = arr[high];
  int i = (low - 1);

  for (int j = low; j < high; j++) {
    if (arr[j] <= pivot) {
      i++;
      swap(arr[i], arr[j]);
    }
  }
  swap(arr[i + 1], arr[high]);
  return (i + 1);
}

장점:

  • 평균적으로 빠른 속도 (O(n log n))
  • 작은 공간 복잡도 (O(log n))

단점:

  • 최악의 경우 O(n^2)의 시간 복잡도 (피벗 요소가 최소 또는 최대값인 경우)
  • 불안정한 알고리즘 (같은 값을 가진 요소들의 순서가 변경될 수 있음)

5. 병합 정렬 (Merge sort)

4

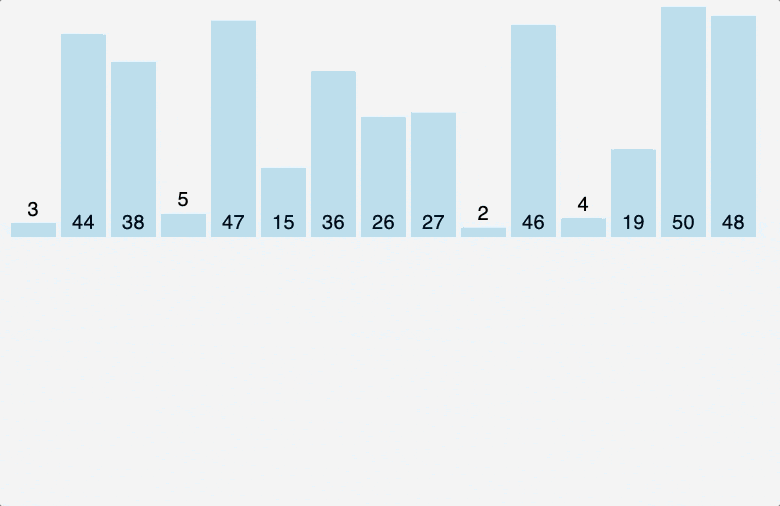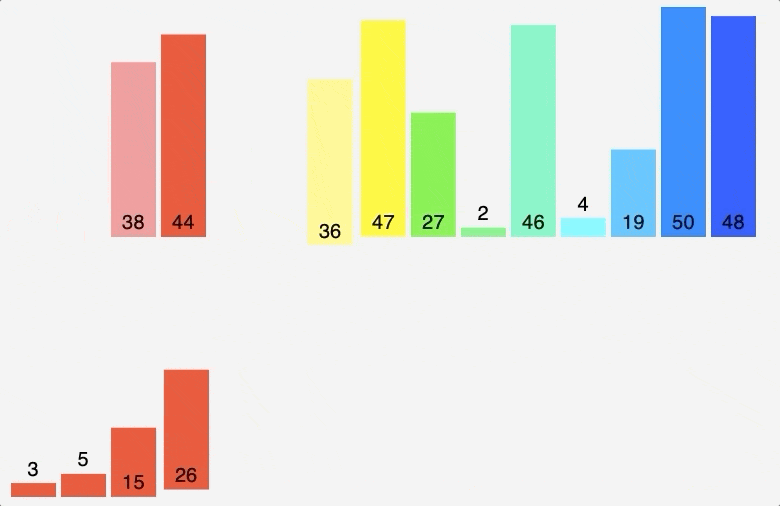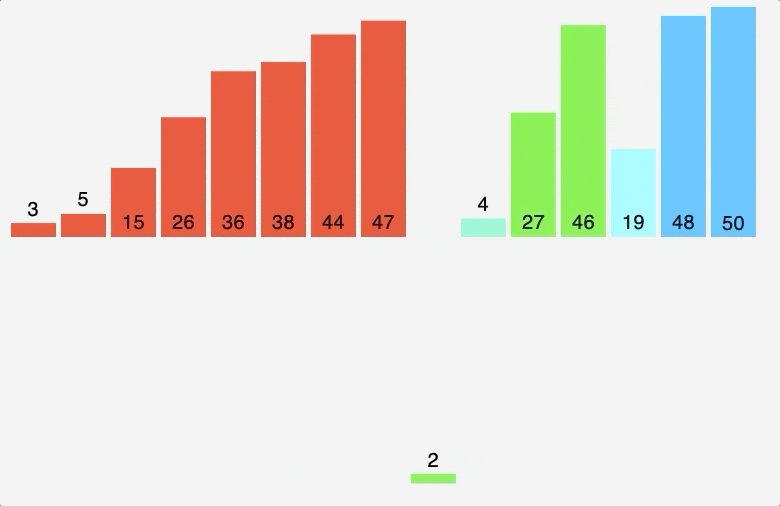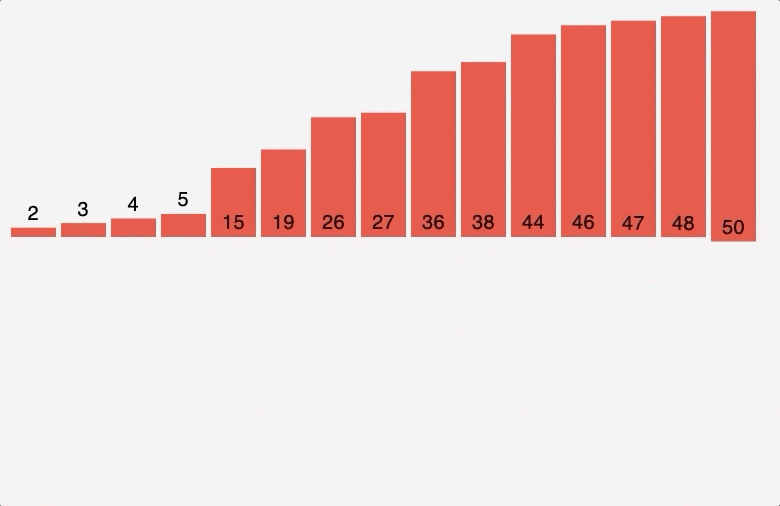
  • 분할: 입력 배열을 절반 크기의 두 개의 부분 배열로 분할합니다.
  • 재귀적 호출: 두 부분 배열을 각각 재귀적으로 병합 정렬 알고리즘을 사용하여 정렬합니다.
  • 합병: 정렬된 두 부분 배열을 하나의 정렬된 배열로 합병합니다.

퀵 정렬과의 차이점 ??

퀵 정렬이 피봇 선택 이후 피봇 기준으로 대소를 비교하는 반면, 병합 정렬은 배열을 원소가 하나만 남을 때 까지 계속 이분할 한 다음, 대소관계를 고려하여 다시 재배열 하며 원래 크기의 배열로 병합한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

""" Best: O(nlogn) Average: O(nlogn) Worst: O(nlogn) | O(n) """
void mergeSort(int arr[], int low, int high) {
  if (low < high) {
    int mid = low + (high - low) / 2;
    mergeSort(arr, low, mid);
    mergeSort(arr, mid + 1, high);
    merge(arr, low, mid, high);
  }
}

void merge(int arr[], int low, int mid, int high) {
  int n1 = mid - low + 1;
  int n2 = high - mid;
  int L[n1], R[n2];

  for (int i = 0; i < n1; i++)
    L[i] = arr[low + i];
  for (int i = 0; i < n2; i++)
    R[i] = arr[mid + 1 + i];

  int i = 0, j = 0, k = low;

장점:

  • 안정적인 알고리즘 (같은 값을 가진 요소들의 순서가 유지됨)
  • 최악의 경우, 평균 경우 모두 O(n log n)의 시간 복잡도
  • 공간 복잡도 O(n)

단점:

  • 퀵 정렬보다 느린 속도 (일반적으로)
  • 추가 공간이 필요합니다.

6. 힙 정렬 (Heap Sort)

5

힙 정렬은 데이터를 힙 구조로 변환하고, 힙에서 최대값을 반복적으로 추출하여 정렬하는 알고리즘입니다. 힙은 특정 조건을 만족하는 완전 이진 트리 구조입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

""" Best: O(nlogn) Average: O(nlogn) Worst: O(nlogn) | O(nlogn) """
void heapSort(int arr[], int n) {
  buildHeap(arr, n);
  for (int i = n - 1; i > 0; i--) {
    swap(arr[0], arr[i]);
    heapify(arr, 0, i - 1);
  }
}

void buildHeap(int arr[], int n) {
  for (int i = n / 2; i >= 0; i--)
    heapify(arr, i, n - 1);
}

void heapify(int arr[], int i, int end) {
  int root = i;
  while (2 * i + 1 <= end) {
    int child = 2 * i + 1;
    if (child + 1 <= end && arr[child] < arr[child + 1])
      child++;
    if (child <= end && arr[root] < arr[child]) {
      swap(arr[root], arr[child]);
      root = child;
    } else {
      return;
    }
  }
}

장점:

  • 평균적으로 빠른 속도 (O(n log n))
  • 공간 복잡도 O(1) (힙 구조만 필요)

단점:

  • 최악의 경우 O(n log n)의 시간 복잡도
  • 불안정한 알고리즘 (같은 값을 가진 요소들의 순서가 변경될 수 있음)

7. 셸 정렬 (Shell Sort)

6

셸 정렬은 삽입 정렬의 변형으로, 데이터 간의 간격을 점차 줄여 삽입 정렬을 반복적으로 수행하는 알고리즘입니다. 간격은 일반적으로 쉘 시퀀스(Shell sequence)라고 불리는 특정 수열을 사용합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

""" Best: O(n) Average: O(n^1.25,1.5) Worst: O(n^2) | O(n) """
void shellSort(int arr[], int n) {
  for (int gap = n / 2; gap > 0; gap /= 2) {
    for (int i = gap; i < n; i++) {
      int current = arr[i];
      int j = i;
      while (j >= gap && arr[j - gap] > current) {
        arr[j] = arr[j - gap];
        j -= gap;
      }
      arr[j] = current;
    }
  }
}

장점:

  • 삽입 정렬보다 빠른 속도 (특히 데이터가 거의 정렬된 경우)
  • 퀵 정렬이나 병합 정렬보다 적은 공간 복잡도 필요

단점:

  • 퀵 정렬이나 병합 정렬보다 느린 속도 (일반적으로)
  • 쉘 시퀀스 선택에 따라 성능이 달라짐

고려사항:

  • 셸 정렬은 일반적으로 데이터가 거의 정렬된 경우에 효율적입니다.
  • 적절한 쉘 시퀀스를 선택하는 것이 중요합니다. 일반적으로 2의 거듭제곱 시퀀스 또는 위에 제시된 시퀀스와 같은 시퀀스를 사용할 수 있습니다.
  • 셸 정렬은 작은 데이터 세트에 효율적이지만, 매우 큰 데이터 세트에는 다른 정렬 알고리즘을 사용하는 것이 더 나을 수 있습니다.

8. 기수 정렬 (Radix Sort)

7

기수 정렬은 데이터의 자릿수를 기준으로 정렬하는 알고리즘입니다. 특히 숫자 데이터를 정렬하는 데 효율적이며, 입력 데이터의 범위가 제한될 때 유용합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

""" Best: O(n) Average: O(n) Worst: O(n)"""
void radixSort(int arr[], int n) {
  int maxDigit = findMaxDigit(arr, n); // 최대 자릿수 계산

  for (int digit = 1; digit <= maxDigit; digit *= 10) {
    countingSort(arr, n, digit);
  }
}

int findMaxDigit(int arr[], int n) {
  int maxDigit = 0;
  for (int i = 0; i < n; i++) {
    int currentDigit = 0;
    int temp = arr[i];
    while (temp > 0) {
      temp /= 10;
      currentDigit++;
    }
    maxDigit = std::max(maxDigit, currentDigit);
  }
  return maxDigit;
}

void countingSort(int arr[], int n, int digit) {
  int count[10] = {0}; // 각 자릿수별 개수 카운팅
  for (int i = 0; i < n; i++) {
    int currentDigit = (arr[i] / digit) % 10;
    count[currentDigit]++;
  }

  int z = 0; // 배열에 삽입할 위치
  for (int i = 0; i < 10; i++) {
    for (int j = 0; j < count[i]; j++) {
      arr[z++] = i * digit;
    }
  }
}
  • findMaxDigit 함수는 배열 내 모든 요소의 최대 자릿수를 찾습니다.
  • radixSort 함수는 자릿수별로 반복적으로 countingSort를 수행합니다.
  • countingSort 함수는 각 자릿수별 개수를 카운팅하고, 카운팅된 개수를 바탕으로 배열을 정렬합니다.

장점:

  • 특정 상황에서 매우 빠른 속도 (O(kn), k는 데이터 자릿수)
  • 안정적인 알고리즘
  • 비교 연산 없이 정렬 가능

단점:

  • 입력 데이터의 범위가 제한되어야 함
  • 문자열이나 실수와 같이 다양한 자릿수를 가진 데이터에는 적합하지 않음

고려사항 :

  • 기수 정렬은 일반적으로 숫자 데이터를 정렬하는 데 효율적입니다.
  • 입력 데이터의 범위가 제한되어야 합니다. 예를 들어, 음수를 포함하는 데이터를 정렬하려면 음수 값을 양수 값으로 변환해야 합니다.
  • 기수 정렬은 매우 큰 데이터 세트에 효율적이지만, 작은 데이터 세트에는 다른 정렬 알고리즘을 사용하는 것이 더 나을 수 있습니다.

9. 카운팅 정렬 (Counting Sort)

8

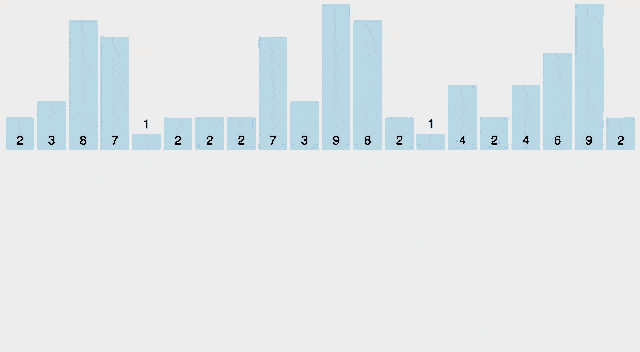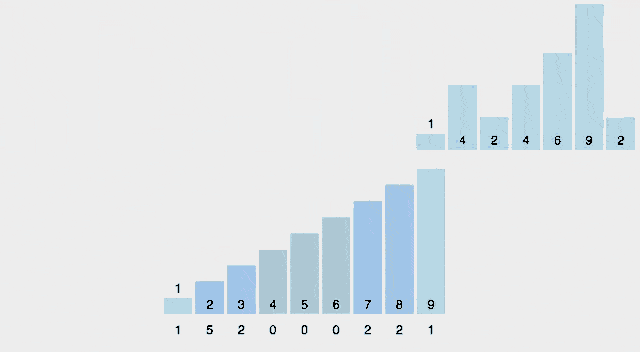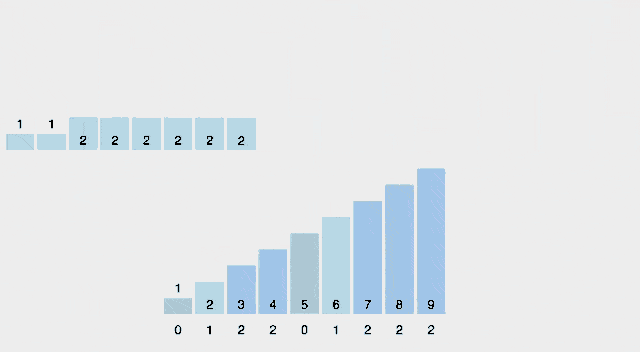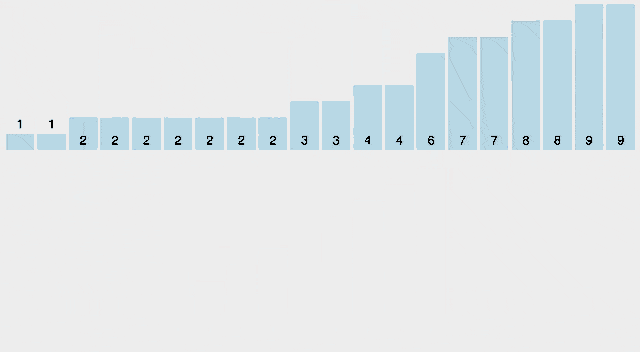
카운팅 정렬은 입력 데이터의 범위가 제한될 때 효율적인 정렬 알고리즘입니다. 데이터의 각 요소에 대한 카운터를 사용하여 데이터를 정렬하는 방식입니다.

1
2
3
4
5
6
7
8
9
10
11

""" Best: O(n) Average: O(n+k) Worst: O(n+k) | O(n+k) """
void countingSort(int arr[], int n, int min, int max) {
  int count[max - min + 1] = {0}; // 카운터 배열 생성
  for (int i = 0; i < n; i++)
    count[arr[i] - min]++; // 각 요소에 대한 카운터 증가

  int z = 0; // 정렬된 배열에 삽입할 위치
  for (int i = min; i <= max; i++)
    for (int j = 0; j < count[i - min]; j++)
      arr[z++] = i; // 카운터 값만큼 동일한 값 삽입
}

장점:

  • 특정 상황에서 매우 빠른 속도 (O(n + k), k는 데이터의 최대값 - 최소값)
  • 안정적인 알고리즘 (같은 값을 가진 요소들의 순서 유지)
  • 비교 연산 없이 정렬 가능

단점:

  • 입력 데이터의 범위가 제한되어야 함
  • 문자열이나 실수와 같이 다양한 값을 가진 데이터에는 적합하지 않음
  • 큰 범위의 데이터에는 공간 비효율적일 수 있음

10. Tim Sort

9

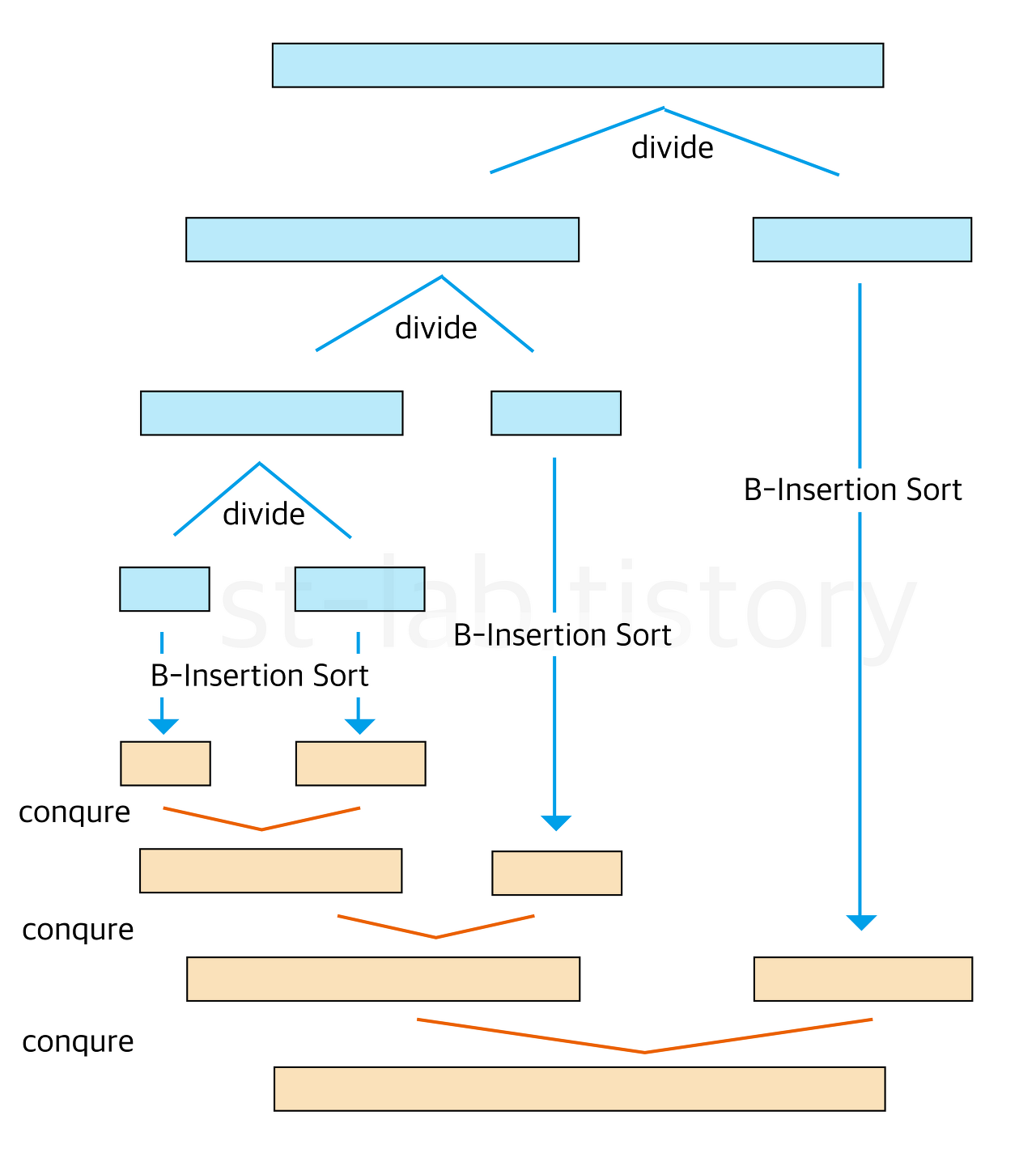
Tim sort는 병합 정렬과 삽입 정렬을 결합한 하이브리드 정렬 알고리즘입니다. Python, Java 등 많은 프로그래밍 언어에서 기본 정렬 알고리즘으로 사용됩니다.

삽입정렬을 결합한 이유??

CPU가 빠른 연산을 위해 사용하는 캐시 메모리에 데이터를 담을 때 적중률을 높이기 위해 사용하는 원리다. 쉽게 말해 최근 참조했던 메모리와 인접한 메모리를 참조할 확률이 높으니 이들을 캐시 메모리에 미리 담아두는 것이며, 삽입정렬은 인접한 메모리와 비교를 반복하기에 참조 지역성의 원리를 잘 만족하고 있다고 할 수 있다. 또 삽입정렬은 원소가 많아질수록 느려지는 단점이 있지만 정렬 수가 적당히 작은 수라면 퀵정렬보다 빨라지는 장점이 있다. Tim Sort는 이러한 삽입정렬의 특성을 활용하여 전체 정렬 대상 원소들을 부분부분(divide)으로 작게 나눈 다음 삽입정렬을 수행하고 병합(conqure)을 수행하면 정렬이 조금 더 빠르지 않을까 하는 아이디어를 기반으로 만들어졌다.

  • 데이터 분할: Tim sort는 입력 데이터를 작은 서브 블록으로 분할합니다. 서브 블록의 크기는 일반적으로 32 또는 64개의 요소입니다.
  • 삽입 정렬: 각 서브 블록은 삽입 정렬을 사용하여 정렬됩니다. 삽입 정렬은 작은 데이터 세트에 효율적이기 때문에 이 단계에서 성능을 향상시킵니다.
  • 병합: 정렬된 서브 블록들을 병합하여 최종적으로 정렬된 배열을 구성합니다. 병합 과정에서 병합 정렬 알고리즘을 사용합니다. 병합 정렬은 큰 데이터 세트에 효율적이기 때문에 이 단계에서 성능을 향상 시킵니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

""" Best: O(n) Average: O(nlogn) Worst: O(nlogn) | O(n) """
void insertionSort(int arr[], int start, int end) {
  for (int i = start + 1; i <= end; i++) {
    int current = arr[i];
    int j = i - 1;
    while (j >= start && arr[j] > current) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = current;
  }
}

void merge(int arr[], int start, int mid, int end) {
  int n1 = mid - start + 1;
  int n2 = end - mid;

  int leftArr[n1], rightArr[n2];

  // 왼쪽 부분 배열 복사
  for (int i = 0; i < n1; i++)
    leftArr[i] = arr[start + i];

  // 오른쪽 부분 배열 복사
  for (int i = 0; i < n2; i++)
    rightArr[i] = arr[mid + 1 + i];

  int i = 0, j = 0, k = start;

  // 왼쪽과 오른쪽 배열을 비교하여 병합
  while (i < n1 && j < n2) {
    if (leftArr[i] <= rightArr[j]) {
      arr[k] = leftArr[i];
      i++;
    } else {
      arr[k] = rightArr[j];
      j++;
    }
    k++;
  }

  // 남은 요소들 채우기
  while (i < n1) {
    arr[k] = leftArr[i];
    i++;
    k++;
  }

  while (j < n2) {
    arr[k] = rightArr[j];
    j++;
    k++;
  }
}

void timSort(int arr[], int n) {
  // 분할 크기 설정 (일반적으로 32 또는 64)
  int m = 32;

  for (int i = 0; i < n; i += m) {
    // 삽입 정렬 수행
    insertionSort(arr, i, std::min(i + m - 1, n - 1));
  }

  int start = 0;
  int mid;
  int end;

  // 병합 단계
  for (int i = m; i < n; i += m) {
    mid = i - 1;
    end = std::min(i + m - 1, n - 1);

    // 병합 수행
    merge(arr, start, mid, end);
    start = end + 1;
  }
}

장점:

  • 평균적으로 빠른 속도: O(n log n)의 시간 복잡도를 가지고 있으며, 일반적으로 다른 정렬 알고리즘들보다 빠른 속도를 제공합니다.
  • 안정적인 알고리즘: 같은 값을 가진 요소들의 순서를 유지합니다.
  • 작은 데이터 세트에 효율적: 삽입 정렬을 사용하여 작은 데이터 세트에 대한 성능을 향상시킵니다.
  • 공간 복잡도 O(n): 병합 정렬에 비해 공간 효율성이 높습니다.

단점:

  • 퀵 정렬보다 느린 속도: 일반적으로 퀵 정렬보다 느린 속도를 제공합니다.
  • 데이터가 거의 정렬된 경우 삽입 정렬만큼 효율적이지 않을 수 있음: 데이터가 거의 정렬된 경우 삽입 정렬만큼 효율적이지 않을 수 있습니다.

참고>

https://velog.io/@leebeanbin/More-details-about-Tim-Sort

정리

10

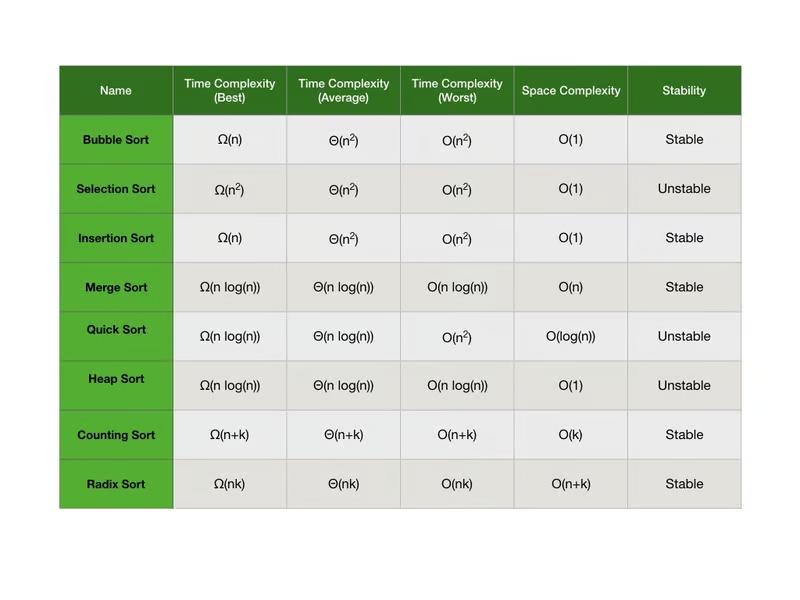
다른종류의 sort를 더 알아보고 싶다면 아래 위키피디아를 참고 하면될거같다. 엄청나게 많은 sort가 존재한다.

https://en.wikipedia.org/wiki/Timsort

참고사이트

https://roytravel.tistory.com/328

CATALOG
    FEATURED TAGS
    CS Algorithm-DFS/BFS Algorithm-구현 Samsung-Coding Algorithm-브루트 포스 Algorithm-DP C++ Algorithm-그리디 알고리즘 Algorithm-백트래킹 C Information Algorithm-이분탐색 BOJ Algorithm-정렬 Python web AI Git IT-Tech-자동차 Notion PJT TroubleShoot etc
    FRIENDS